문제 설명
매운 것을 좋아하는 Leo는 모든 음식의 스코빌 지수를 K 이상으로 만들고 싶습니다. 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 Leo는 스코빌 지수가 가장 낮은 두 개의 음식을 아래와 같이 특별한 방법으로 섞어 새로운 음식을 만듭니다.
섞은 음식의 스코빌 지수 = 가장 맵지 않은 음식의 스코빌 지수 + (두 번째로 맵지 않은 음식의 스코빌 지수 * 2)
Leo는 모든 음식의 스코빌 지수가 K 이상이 될 때까지 반복하여 섞습니다.
Leo가 가진 음식의 스코빌 지수를 담은 배열 scoville과 원하는 스코빌 지수 K가 주어질 때, 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 섞어야 하는 최소 횟수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
- scoville의 길이는 2 이상 1,000,000 이하입니다.
- K는 0 이상 1,000,000,000 이하입니다.
- scoville의 원소는 각각 0 이상 1,000,000 이하입니다.
- 모든 음식의 스코빌 지수를 K 이상으로 만들 수 없는 경우에는 -1을 return 합니다.
입출력 예
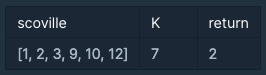
입출력 예 설명
- 스코빌 지수가 1인 음식과 2인 음식을 섞으면 음식의 스코빌 지수가 아래와 같이 됩니다.
새로운 음식의 스코빌 지수 = 1 + (2 * 2) = 5
가진 음식의 스코빌 지수 = [5, 3, 9, 10, 12] - 스코빌 지수가 3인 음식과 5인 음식을 섞으면 음식의 스코빌 지수가 아래와 같이 됩니다.
새로운 음식의 스코빌 지수 = 3 + (5 * 2) = 13
가진 음식의 스코빌 지수 = [13, 9, 10, 12]
모든 음식의 스코빌 지수가 7 이상이 되었고 이때 섞은 횟수는 2회입니다.
풀이 코드
import heapq
def solution(scoville, K):
answer = 0
heapq.heapify(scoville)
while True:
min_sco = heapq.heappop(scoville)
if min_sco < K and len(scoville) == 0:
answer = -1
break
if min_sco >= K:
break
else:
next_sco = heapq.heappop(scoville)
heapq.heappush(scoville, min_sco + next_sco * 2)
answer += 1
return answer힙을 이용해서 풀이할 수 있다.
힙에서 가장 작은 것 두 가지를 뽑아 주어진 식에 맞게 구성하면 된다.
1) heappop 이후에 힙에 남은 것이 없고, 값이 K 보다 작은 경우를 고려하고,
2) 가장 작은 값마저 K보다 크거나 같은 경우를 고려해주면 쉽게 풀이할 수 있다.
'🐍 코딩테스트 대비 : PS' 카테고리의 다른 글
| [프로그래머스] 단어 변환 (level3, python) (0) | 2022.09.13 |
|---|---|
| [프로그래머스] 주식가격 (level2, python) (1) | 2022.09.13 |
| [프로그래머스] [3차] 압축 (level2, python) (0) | 2022.09.12 |
| [프로그래머스] 타겟 넘버 (level2, python) (0) | 2022.09.12 |
| [프로그래머스] 네트워크 (level3, python) (0) | 2022.09.12 |
![[프로그래머스] 더 맵게 (level2, python)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbc49q0%2FbtrLYk5Bf3J%2FgtKBMon28tYm9UaKn9v78K%2Fimg.png)